I’m back again to my Algorithms and Data Structure journey. This time I will write a post for each chapter or topic.

Min/Max Heap definition

A Max Heap is a binary tree where it’s respected exactly one condition

Every node should be greater than it’s childs

And the same rule is applied for Min Heap

Every node should be smaller than it’s childs

Data structure

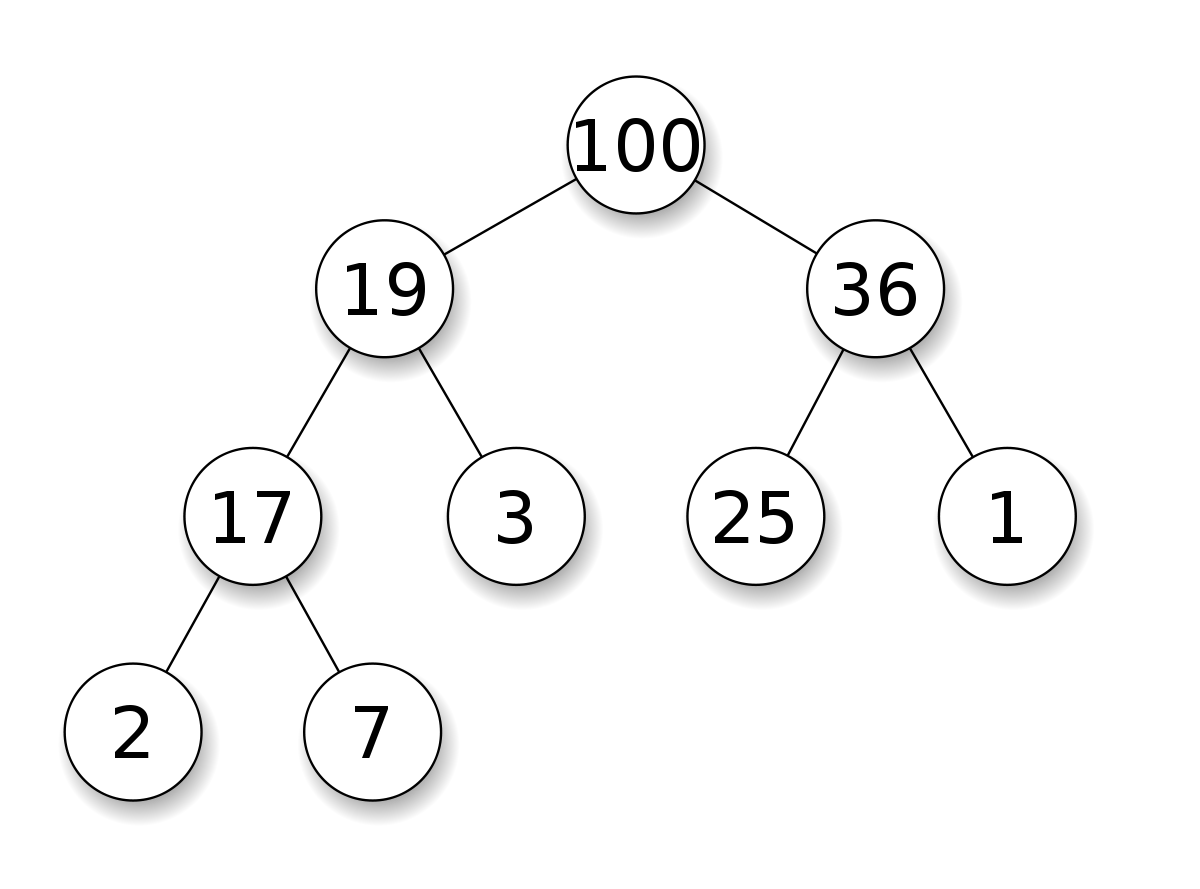
As a data structure, heap is a nearly complete binary tree. The tree is completely filled on all levels, except last one. Last once should be filled from left to right.

Code

Parent/Left/Right

Since Golang has 0-indexed arrays, implementation of these methods may look a little bit different. You can do cleaner implementation, by not using 0-element.

// left returns parent index for i-th node
func parent(i int) int {
	return ((i - 1) >> 1)
}

// left returns left child index for i-th node
func left(i int) int {
	return (i << 1) + 1
}

// right returns right child index for i-th node
func right(i int) int {
	return (i << 1) + 2
}

MaxHeapify

// maxHeapify places i-th node in the right position in it's subtree
func maxHeapify(i int, heap []int) {
	left := left(i)
	right := right(i)
	max := i

	if left < len(heap) && heap[left] > heap[i] {
		max = left
	}
	if right < len(heap) && heap[right] > heap[max] {
		max = right
	}

	if max != i {
		heap[i], heap[max] = heap[max], heap[i]
		maxHeapify(max, heap)
	}
}

MaxHeap

// maxHeap rearranges array into a max heap
func maxHeap(heap []int) {
	for i := len(heap) - 1; i >= 0; i-- {
		maxHeapify(i, heap)
	}
}

HeapSort

Using all functions defined above, we can easily do a sorting O(nlgn). Since we know that we have biggest number placed at index-0, we can swap it with the last item from the heap and call maxHeapify to rearrange node in it’s subtree.

// heapSort sorts an array using a heap
func heapSort(arr []int) {
	maxHeap(arr)
	for l := len(arr) - 1; l > 0; l-- {
		arr[0], arr[l] = arr[l], arr[0]
		arr = arr[:l]
		maxHeapify(0, arr)
	}
}